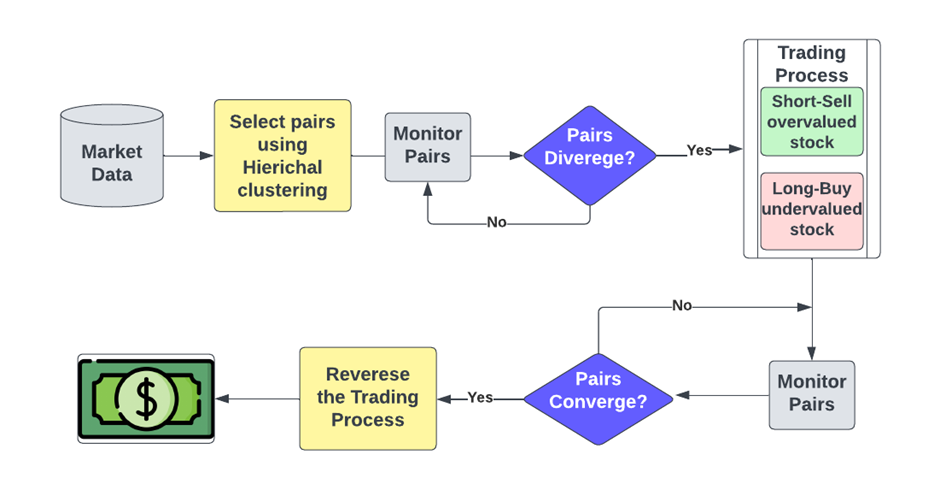
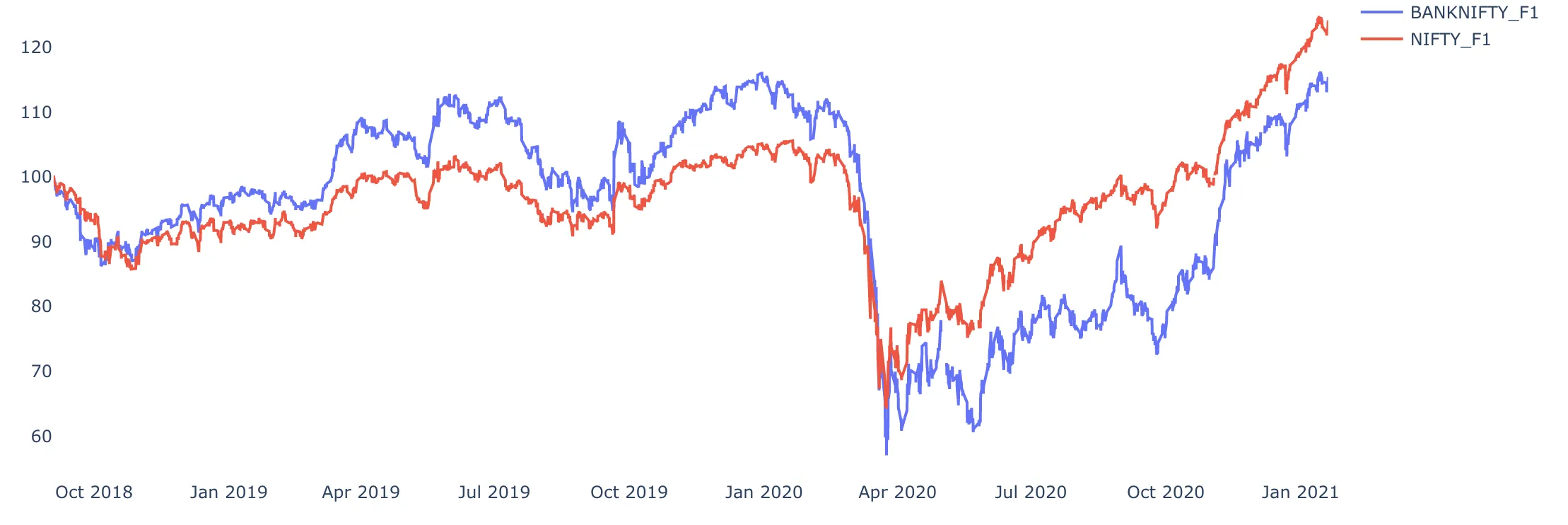
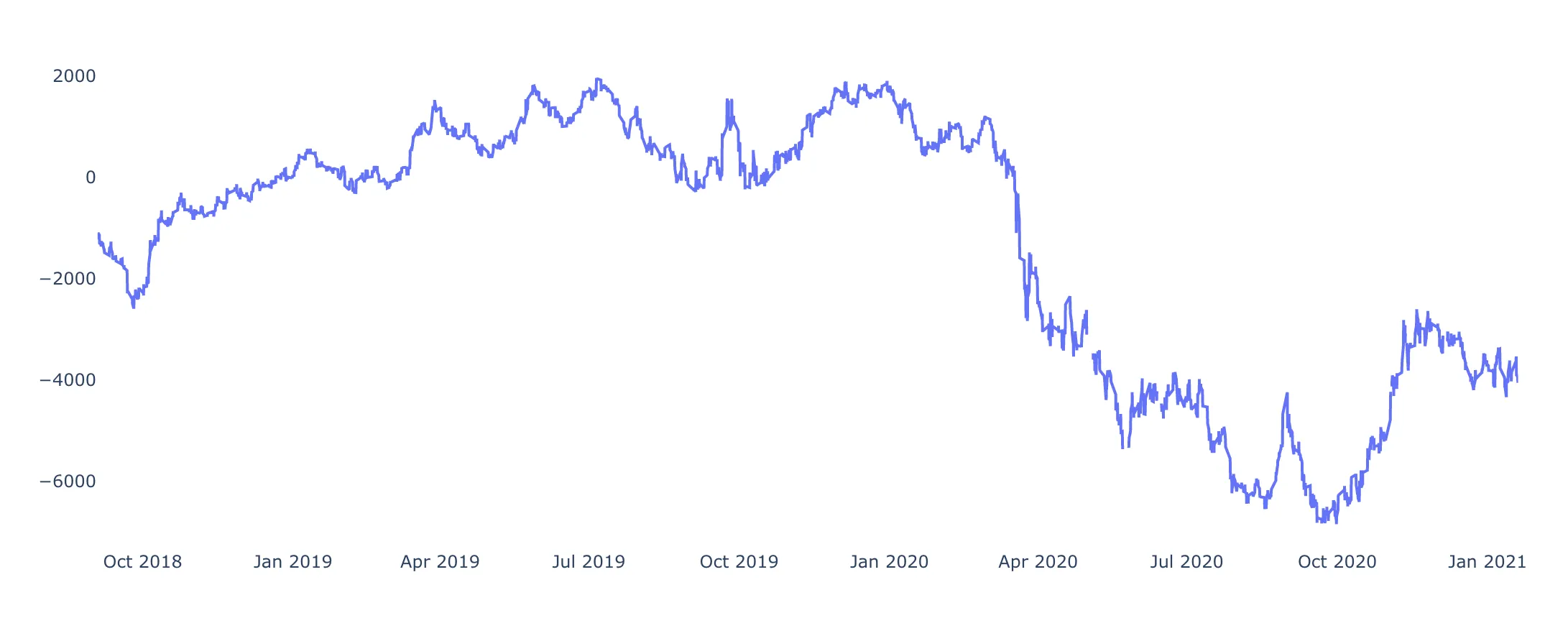
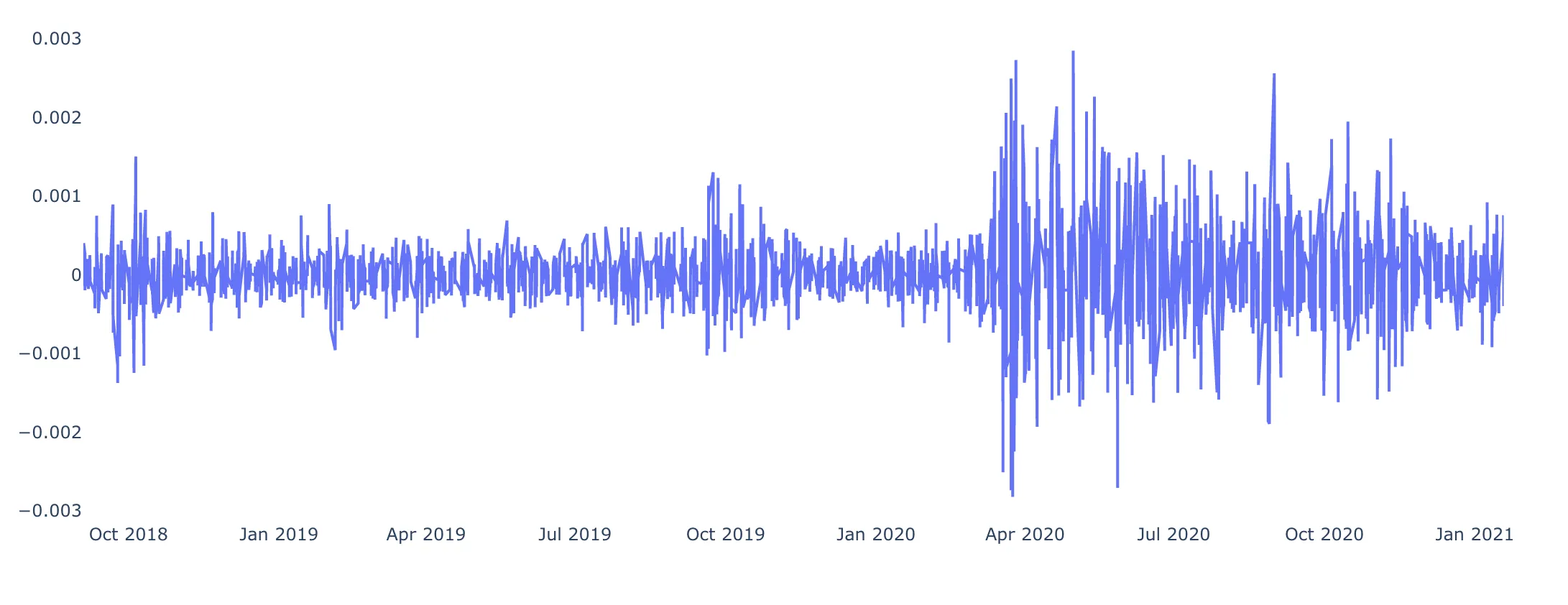
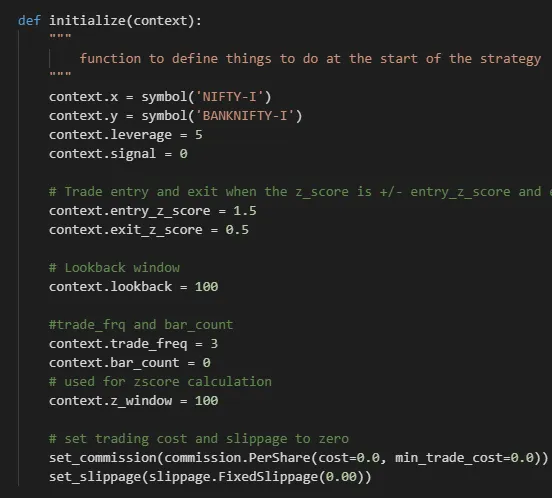
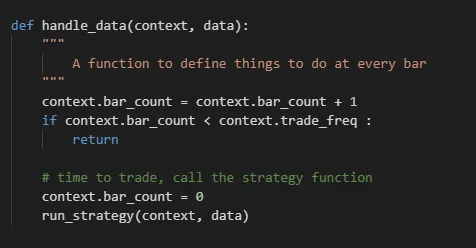
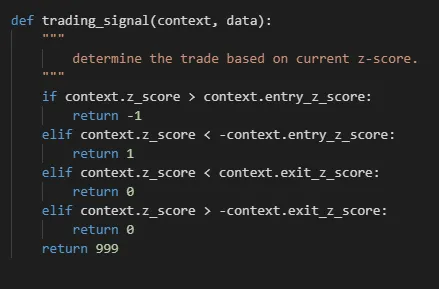
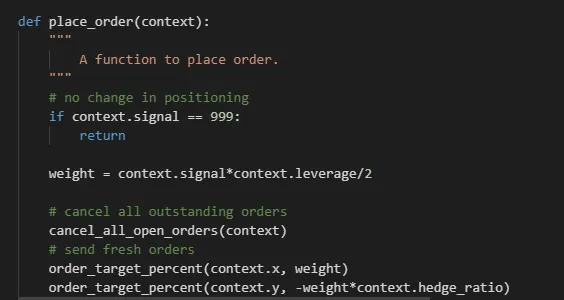
- Tools

Get your
financial
Advise - Services

Get your
financial
Advise - About
-
News & Blogs
-
Start Investing
Find the
Perfect Portfolio
- Sign In